Messtechnik Im Zeit- und Frequenzbereich messen

Ingenieure, die mit schneller Digitalkommunikation zu tun haben, beobachten und analysieren Signale und Systeme normalerweise im Zeitbereich. Systeme und Signale können aber auch als Funktion der Frequenz charakterisiert werden. Das ist das Reich der Hochfrequenz(HF)-Ingenieure. Je mehr nun die Digitaltechnik in den Bereich GBit/s vorstößt, desto mehr müssen Digitaltechnikingenieure einsehen, dass Messungen im Frequenzbereich wertvolle Einsichten in das Verhalten eines Systems im Zeitbereich geben. HF-/Mikrowellen-
ingenieure andererseits werden mehr und mehr zu Dienstleistern für Digitalanwendungen und müssen dort für Signalintegrität sorgen. Dafür müssen sie Messungen im Zeitbereich beherrschen. Was alle beachten sollten ist, dass Signalmessungen in einem Bereich auch mit dem zusammenhängen, was im jeweils anderen Bereich zu beobachten ist.

Blick in zwei Welten

Für viele Ingenieure kommen die digitale und die HF-Welt im Laufe eines Berufslebens wieder zusammen: Wenn normale serielle Computerbusse Datenraten von 2,5 oder sogar
>10 GBit/s erreichen, ist es offensichtlich, dass sich Digitaltechnik und HF-Technik einander nähern. Was bedeutet das aber für den Hochfrequenz-Ingenieur? Obwohl nur Einsen und Nullen übertragen werden, sind seine Kenntnisse und Fertigkeiten bezüglich Wellenleitung, Rauschen, PLLs (Phase-Locked Loop) und Nachrichtentechnik wesentlich für die erfolgreiche Entwicklung von Digitalsystemen. Der Digitalingenieur muss sich immer noch mit Logik, Codierung, Fehlererkennung und -korrektur auskennen. Heute aber spielen diese Fertigkeiten nicht nur eine Rolle bei der Korrektur von Daten, die auf fehlerbehafteten Medien gespeichert werden, sondern auch bei Kommunikationsverfahren mit hohen Übertragungsraten, wo die Signalgüte unter Umständen schon schlechter wird, wenn Sender und Empfänger nicht mal einen Meter auseinanderstehen.

Im Zeit- wie im Frequenzbereich denken

Eine wichtige Fertigkeit der Ingenieure besteht darin, sowohl im Zeitbereich als auch im Frequenzbereich zu denken. Betrachtet etwa der Digitalingenieur einen digitalen Bitstrom auf einem Oszilloskop und hat eine Vorstellung davon, wie das Spektrum dieses Bitstroms aussieht, dann gibt ihm das einen wichtigen Einblick in die Integrität – oder Nicht-Integrität – dieses Signals. Misst er den Frequenzgang oder die Bandbreite eines Kommunikationskanals und hat dabei im Hinterkopf, wie der Bitstrom im Zeitbereich davon beeinflusst wird, kann er erkennen, ob dieser Kanal funktioniert oder nicht.

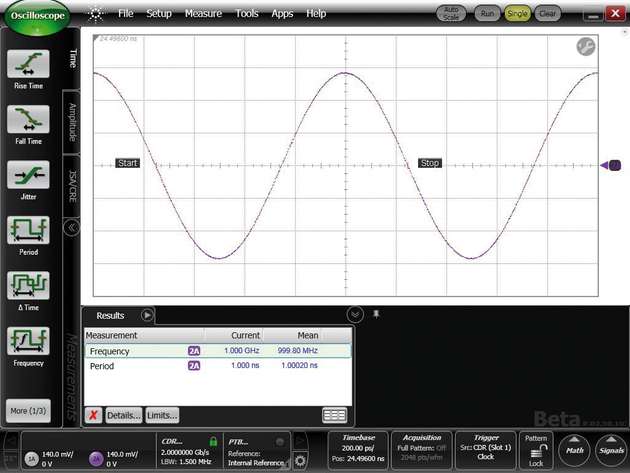
Ein elektrisches Signal ist als Diagramm – Spannung über der Zeit – darstellbar und wird als Signal auf einem Oszilloskop betrachtet. Das gleiche Signal kann aber auch als Spektrum – Amplitude über der Frequenz – angezeigt werden; so erscheint es auf einem Spektrumanalysator. Mathematisch wird mittels einer Fourier-Transformation die Zeit in Frequenz umgerechnet. Dieses Verfahren überträgt ein Signal oder eine Funktion vom Zeitbereich in den Frequenzbereich. Es zeigt, welche Teilfrequenzen in einer zeitlichen Messkurve stecken. Ein einfaches Beispiel hierfür ist ein Sinus- und ein Rechtecksignal.Abbildung 1a zeigt eine Sinuskurve mit einer Periodendauer von 1 ns. Welche Frequenzen stecken in diesem Signal? Dieses Beispiel ist ganz einfach: Das Signal enthält nur eine einzige Frequenz von 1 GHz. Und wie sieht das mit einem Rechtecksignal mit 1 ns Periodendauer aus? Ein Digitalingenieur würde erwarten, dass es auch eine Frequenz von 1 GHz enthält. Das stimmt auch, aber daneben enthält es noch andere Frequenzen, nämlich 3 GHz, 5 GHz, 7 GHz und so weiter. Das Signal ist zusammengesetzt aus dem Grundton, dem Kehrwert der Periodendauer, und seinen ungeraden Harmonischen. Mit wachsender Frequenz der Harmonischen sinkt deren
Amplitude.

Wird die Kurvenform eines Signals im Zeitbereich komplizierter, wird auch das zugehörige Spektrum im Frequenzbereich komplizierter. Ein Spektrum eines Digitalsignals mit
2 GBit/s folgt einer Funktion sin(x)/x, welches ebenfalls keinerlei Spektralgehalt bei 2 GHz und den Harmonischen von
2 GHz. Ein Rechtecksignal von 1 GHz entspricht nämlich einem 2-GBit/s-Signal mit dem Signalinhalt 1-0-1-0-1-0, und beide weisen keine Teilfrequenzen bei geradzahligen Vielfachen von 2 GHz auf. Wenn das Spektrum eines Signals bekannt ist, also seine Frequenzkomponenten, kann der Ingenieur daraus seine Signalform im Zeitbereich rekonstruieren, also Amplitude über der Zeit. Hierzu benutzt er die inverse Fourier-Transformation. Das funktioniert bei allen Beispielen aus Abbildung 1: Für eine genaue Rekonstruktion braucht er allerdings noch Informationen über die Phasenlage – das ist in Abbildung 1 nicht dargestellt.

Nicht ideale Kurvenformen

Betrachtet der Ingenieur Digitaldaten auf einem Oszilloskop, würde er eine Folge praktisch rechteckiger Impulse erwarten, die für Einsen stehen, und die Abwesenheit von Impulsen, was für logische Nullen steht. Bei einem schnellen Digitalsignal sieht er das so aber nicht. Die Einsen sind dort längst nicht so rechteckig wie erwartet, und die Nullen sind keine glatten Linien auf Nullniveau. Stattdessen sieht er erheblich geneigte Flanken, die einen Gutteil der Bitzeit in Anspruch nehmen. Wechselt ein Signal von 0 auf 1, schwingt es möglicherweise über, bevor es sich auf dem Nennpegel beruhigt.

Mittels Filtertheorie kann erklärt werden, warum diese Kurvenformen längst nicht ideal sind. Entwickelt der Ingenieur ein Filter, geht es primär darum, einen bestimmten Frequenzbereich durchzulassen und einen anderen Frequenzbereich zu sperren. Aus dem oben dargestellten Zusammenhang der Kurvenform eines Signals mit seinen Frequenzkomponenten folgt, dass sich die Kurvenform eines Signals vermutlich ändert, wenn es ein Filter durchläuft. Immer, wenn sich das Spektrum eines Signals ändert, ändert sich auch die Kurvenform im Zeitbereich. Was passiert, wenn das 1-GHz-Rechtecksignal aus Abbildung 1b durch ein Tiefpassfilter geschickt wird, das Frequenzen bis 2 GHz durchlässt und Frequenzen über 2 GHz sperrt? Als einzige Frequenzkomponente würde
1 GHz durchgelassen, und aus dem Rechtecksignal würde ein Sinussignal werden. Was würde passieren, wenn das Filter alles bis 4 GHz durchlassen und Frequenzen über 4 GHz sperren würde? Nun würde das Signal hinter dem Filter eine Komponente mit 1 GHz aufweisen und eine mit 3 GHz. Dieses Signal wäre dann zwar keine Sinuskurve, aber auch kein 1-GHz-Rechtecksignal mehr.

Abbildung 2 zeigt, was das Tiefpassfilter aus dem Rechtecksignal macht: Die Flanken sind flacher, „Böden" und „Dächer" des Rechtecksignals sind nicht mehr eben. Das Signal sieht jetzt aus, als sei eine langsame Sinuskurve, ein 1-GHz-Ton, mit einer schnelleren, einem 3-GHz-Ton, überlagert. Das Filter arbeitet also wie erwartet. Die obigen Beispiele waren recht einfach. Die Wirklichkeit ist etwas komplizierter. Ingenieure müssen nämlich etliche Dinge zusätzlich beachten:

• Laufen alle Frequenzen gleich schnell durch das Filter? Wenn nicht, wie verändert das die Kurvenform?

• Unterliegen alle Signalfrequenzen im Durchlassband der gleichen Dämpfung? Einige Filterdesigns weisen im Durchlassband eine Welligkeit auf – eine sich ändernde Dämpfung –, andere zeigen eine Überhöhung kurz vor der Grenzfrequenz. Wie verändert das die Kurvenform?

• Ändert man das Signalspektrum durch Dämpfung, Verstärkung oder Änderung der Phasenbeziehung zwischen den Spektralelementen des Signals, ändert sich die Kurvenform. Ist diese Verzerrung der Kurvenform tolerabel?

Bei der Konstruktion eines Filters muss man wissen, ob der Zeitbereich oder der Frequenzbereich Priorität hat. Einige Filterformen bieten etwa eine exzellente Dämpfung im Sperrbereich auf Kosten einer Verzerrung der Kurvenform.

Signal und Bitfehlerrate

Ein digitales Kommunikationssystem kann nur ordentlich arbeiten, wenn der Empfänger Einsen korrekt als Einsen interpretiert und Nullen als Nullen. Einen Fehler bei dieser Interpretation nennt der Ingenieur einen Bitfehler. Die Systemleistung bewertet er allgemein nach der Bitfehlerrate (BER), also dem Verhältnis von fehlerhaft empfangenen zu allen empfangenen Bits. Ein typischer Wert ist ein Fehler pro Billion empfangener Bits. Eine niedrige BER wird durch einen deutlichen Unterschied zwischen den Logikpegeln für 0 und 1 erreicht und weiterhin dadurch, dass die Entscheidung, ob ein Bit 0 oder 1 ist, zeitlich möglichst weit entfernt von Pegelwechseln stattfindet. Der „Entscheidungszeitpunkt“ liegt üblicherweise in der Mitte der Bitzeit und in der Mitte zwischen den beiden Logikpegeln. Weicht das Signal vom Ideal ab und kommt den Grenzen nahe, steigt die Wahrscheinlichkeit einer Fehlentscheidung. Wenn das Signal also nicht die ideale, rechteckige Form aufweist, ist die BER in Gefahr. In sehr schnellen digitalen Kommunikationsnetzen liegt die Verzerrung der Signalform oft daran, dass sich das Signalspektrum beim Durchlauf des Signals durch das System ändert. Die oben besprochenen Überlegungen zu Filtern gelten sinngemäß hier auch.

Ursache einer verzerrten Kurvenform

Will man die Ursache einer Verzerrung der Kurvenform finden, fällt der erste Verdacht immer auf den Übertragungskanal, also das Medium, das das Signal vom Sender zum Empfänger überträgt – etwa eine Leiterbahn in einem PC oder ein Stück Glasfaser. Die meisten Übertragungskanäle wirken wie Tiefpässe. Es gibt verschiedene Gründe für die Dämpfung hoher Frequenzen beim Durchlauf eines Signals durch einen Übertragungskanal. Auf Leiterplatten oder in Kabeln weist das Isolationsmaterial möglicherweise bei höheren Frequenzen höhere Verluste auf als bei niedrigen. Höhere Frequenzen nutzen tendenziell nur die äußere Schicht eines Leiters und nicht den gesamten Querschnitt. Das erhöht den effektiven Widerstand und somit die Dämpfung. Selektive Dämpfung des höherfrequenten Teils des Spektrums eines Digitalsignals wirkt so, wie oben anhand eines Rechtecksignals demonstriert, das durch einen Tiefpass läuft: Die Flanken werden flacher. Bei einer Glasfaser entsteht Hochfrequenzverlust dadurch, dass das Licht, das ein Digitalsignal trägt, unterschiedlich lange Wegstrecken zurücklegt. In einer Glasfaser kann es gleichzeitig mehrere Wege der Lichtausbreitung entlang der Faser geben. Digitaldaten, übertragen in Form von Lichtimpulsen, kommen dann zeitlich gestreckt beim Empfänger an. Die gestreckten Lichtimpulse entsprechen elektrischen Impulsen nach Durchlauf durch einen Tiefpass: Ihre Flanken sind flacher geworden und ihre Signalform ist verzerrt. Insgesamt ist die Signalqualität verschlechtert, die Wahrscheinlichkeit eines Bitfehlers steigt.
Weitere Informationen zu Keysight Technologies finden Sie im Business-Profil auf der Seite 48.