Der wohl wichtigste Systemparameter nachhaltiger Energieübertragung, egal ob kabel- und kontaktgebunden oder gar kontaktlos, ist der Wirkungsgrad als Verhältnis zwischen Ausgangs- zu Eingangswirkleistung. Der Wirkungsgrad ist abhängig vom Übertragungssystem selbst, aber auch von der gewählten Außenbeschaltung wie zum Beispiel der belastenden Impedanz. Durch eine optimierte Dimensionierung dieser Außenbeschaltung kann der Wirkungsgrad maximieret werden.
Mit Kenntnis des maximal erreichbaren Wirkungsgrades wird es möglich, Übertragungssysteme zu charakterisieren und zu vergleichen. In [2, 3] wurde hierzu für kontaktlose, induktive Systeme bereits eine „figure of merit“ (FOM) vorgestellt, welche aus der Güte der Induktivitäten sowie der Kopplung berechnet werden konnte. Diese Größe geht jedoch von einem vereinfachten Übertragungsmodell und stets von einer induktiven Energieübertragung aus. Gleichzeitig wird keine Aussage über den Wirkungsgradabfall bei abweichendem Lastwiderstand gemacht.
Anhand eines vollständigen Übertragungsmodells des passiven, linearen, zeitinvarianten und reziproken Übertragungssystems wird im Folgenden die Übertragungsgüte vorgestellt. Diese gibt sowohl Auskunft über den maximal erreichbaren Wirkungsgrad, aber auch über den Wirkungsgradabfall bei variablem Lastwiderstand. Darüber hinaus ist sie nicht auf induktiv gekoppelte Systeme beschränkt, sondern kann bei einer Vielzahl von Übertragungssystemen sowohl kontaktgebunden als auch kontaktlos Anwendung finden.
Vorstellung der Übertragungsgüte
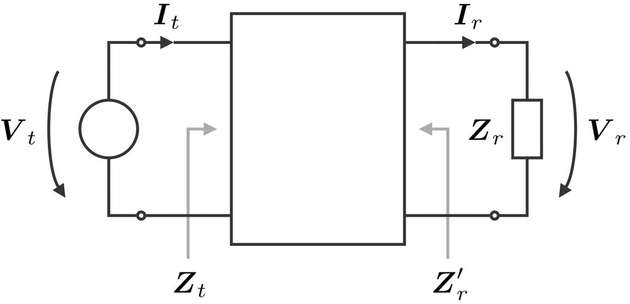
Eine Energiequelle speist im Allgemeinen Leistung in ein Übertragungssystem ein und eine Energiesenke entnimmt einen Teil dieser Leistung. Diesen Sachverhalt veranschaulicht Abbildung 1. Wird nun davon ausgegangen, dass das Übertragungssystem zwischen Quelle und Senke durch ein lineares zeitinvariantes (LTI)-Netzwerk beschrieben werden kann und gleichzeitig die Senke durch eine Impedanz approximierbar ist, bietet sich die Beschreibungsform der Zweitortheorie an. Selbst bei vielen nichtlinearen Systemen ist diese nach Anwendung bekannter Linearisierungsverfahren wie zum Beispiel der harmonischen Gleichrichterapproximation [4] zulässig.
Das LTI-Übertragungssystem kann entsprechend der in Abbildung 1 gewählten Zählpfeilrichtungen durch das Gleichungssystem (1) beschrieben werden.
(1)
Spannungen und Ströme sind hier in komplexen Amplituden angegeben. Die Elemente der Matrix sind Impedanzen, weshalb von der Impedanzmatrix gesprochen wird. Sie können rechnerisch oder auch messtechnisch ermittelt werden.
An dieser Stelle ist bereits der erste Unterschied zur „figure of merit“ erkennbar. Die Abhandlungen [2, 3] gehen davon aus, dass die Koppelimpedanz Ztr durch lediglich eine Reaktanz angenähert werden kann. Diese Näherung ist bei vielen induktiven Übertragungssystemen tatsächlich oft zulässig, jedoch bei alternativen Übertragungsverfahren wie der kapazitiven oder der leitungsgebundenen Energieübertragung nicht zwingend erfüllt.
Soll nun von dem Übertragungssystem aus Abbildung 1 der Wirkungsgrad der Energieübertragung bestimmt werden, ist nach einer Aufteilung aller Impedanzen in (1) entsprechend Z = R + jX sowie dem Zusammenhang
(2)
lediglich die Kenntnis des Betrages der Stromübertragungsfunktion und des Realteils der Eingangsimpedanz erforderlich. Nach Bestimmung dieser Größen [1] folgt der Wirkungsgrad zu
(3)
mit
(4)
Durch die Unabhängigkeit des Wirkungsgrades (3) vom Imaginärteil Xtt lässt sich feststellen, dass der Wirkungsgrad ebenfalls unabhängig von einer eventuell vorgeschalteten Quellreaktanz ist. Demzufolge kann der Wirkungsgrad bei vorgegebener Frequenz lediglich durch eine gezielte Dimensionierung der Ausgangsimpedanz und nicht durch eine Quellimpedanz optimiert werden.
Aus Gleichung (3) ist ersichtlich, dass zur Maximierung des Wirkungsgrades der Imaginärteil der belastenden Impedanz Xr zu Xr,η = γ gewählt werden muss. So lässt sich der linke Teil der Summe im Nenner streichen. Wird dies berücksichtigt, kann auch der zur Maximierung benötigte Realteil ermittelt werden. Nach [1] gilt für den zur Maximierung des Wirkungsgrades erforderlichen Realteil
(5)
Rr und Xr in Gleichung (3) liefern nach der Definition einer Übertragungsgüte
(6)
einen mit vorhandenem Übertragungssystem, unter optimalen Bedingungen maximal erreichbaren Wirkungsgrad. Es gilt
(7)
Wird in Gleichung (4) davon ausgegangen, dass Rtr = 0 ist, gilt in Bezug auf [2, 3] und der bekannten FOM der Zusammenhang
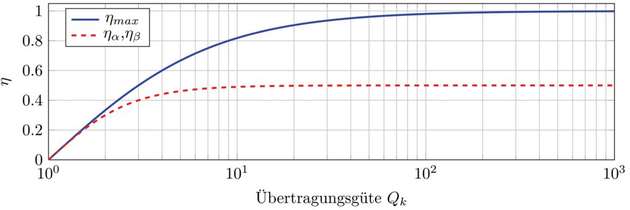
Abbildung 2 zeigt in Blau den maximal erreichbaren Wirkungsgrad, aufgetragen über der Übertragungsgüte. Die Definitionen von (4) eingesetzt in Gleichung (6) macht die Übertragungsgüte zu einer Größe, mit welcher unterschiedlichste Energieübertragungssysteme verglichen werden können. Nachfolgend zwei Beispiele:
Induktive, kontaktlose Energieübertragungssyteme erreichen problemlos Übertragungsgüten zwischen 10 und 100. Kapazitive Übertragungssysteme haben eine tendenziell höhere Übertragungsgüte.
Durch eine Bestimmung der Impedanzmatrix mittels Leitungstheorie lässt sich zu einem Erdkabel (Typ: 3xN2XSEY CU 185 mm2) zur direkten Verbindung zwischen Stuttgart und München (~190 km) eine Übertragungsgüte von 7.8 bestimmen. Eine entsprechende Freilandleitung erreicht beispielhaft eine Übertragungsgüte von 280.
Variation der Last
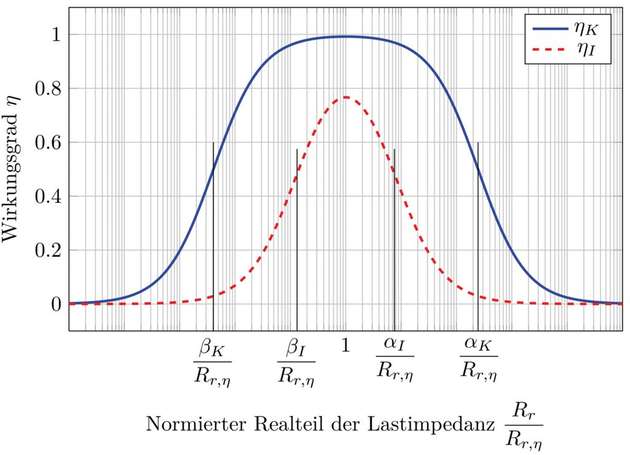
Nachdem mit der vorangegangenen Betrachtung bekannt ist, dass der Wirkungsgrad eines Übertragungssystems lediglich durch die Wahl einer geeigneten Lastimpedanz maximiert werden kann und mit Rr,η und Xr,η Real- und Imaginärteil dieser Impedanz gefunden sind, soll nachfolgend geprüft werden, welchen Einfluss eine Variation des Realteils dieser Lastimpedanz auf den Wirkungsgrad der Energieübertragung hat. Hierzu wird in Abbildung 3 der Wirkungsgrad zweier Übertragungssysteme mit einer Übertragungsgüte von 7.8 (rot) beziehungsweise 280 (blau) über einem normierten Realteil der Lastimpedanz Rr aufgezeichnet.
Zum einen kann bestätigt werden, dass beide Systeme beim Realteil der Lastimpedanz (5) ein Maximum aufweisen und entsprechend Gleichung (7) einen Wirkungsgrad von 75 Prozent respektive 99 Prozent erreichen können. Gleichzeitig ist erkennbar, dass der Variationsbereich der Last, in welchem ein vergleichsweise hoher Wirkungsgrad erreicht werden kann, stark von der Übertragungsgüte abhängig ist. Das System höherer Übertragungsgüte (blau) ist bei variabler Last deutlich besser zur Energieübertragung geeignet, als das System niedriger Übertragungsgüte.
Übertragungsbandbreite
In der vorangegangenen Betrachtung wurden bereits die Größen α und β und in Gleichung (6) der Einfluss auf die Übertragungsgüte vorgestellt. Diese sind ebenfalls in Abbildung 3 eingezeichnet. Sie begrenzen einen Widerstandsbereich ( β ≤ Rr ≤ α), in welchem ein vergleichsweise hoher Wirkungsgrad erreicht wird. Die minimalen Wirkungsgrade in den Bereichsgrenzen ηα und ηβ sind identisch und bestimmbar zu
(9)
Die Abhängigkeit der Gleichung (9) von der Übertragungsgüte ist zusätzlich in Abbildung 2 eingezeichnet. Bei großen Übertragungsgüten nimmt ηα und ηβ einen Wert von näherungsweise 50 Prozent an. Bei kleineren Übertragungsgüten nimmt der Grenzwirkungsgrad wie auch der maximal erreichbare Wirkungsgrad ab. Aufgrund dieser Zusammenhänge liegt es nahe, eine Übertragungsbandbreite zu definieren. Normiert auf Rr,η gilt
(10)
Aus Gleichung (6) ist bekannt, dass die quadrierte Übertragungsgüte dem Quotienten aus den Bereichsgrenzen alpha und beta entspricht. Demnach enthält die Übertragungsgüte alle Informationen, welche eine Aussage über den Variationsbereich der Last zulassen. Dies bestätigt auch Gleichung (10). Mit wachsender Übertragungsgüte wächst der Lastvariationsbereich mit hohem Wirkungsgrad an.
Zusammenfassung
Von sämtlichen LTI-Energieübertragungssystemen kann eine Übertragungsgüte bestimmt werden, welche Aufschluss über den Wirkungsgrad liefert und gleichzeitig einen Vergleich unterschiedlichster Systeme zulässt. Zusätzliche Informationen wie zum Beispiel die Zusammenhänge bei im Gegensatz zu (9) beliebig definierbarem Grenzwirkungsgrad sind in der Abhandlung [1] zu finden.
Literatur
[1] D. Huwig, „Energieübertragung durch Nahfeldkopplung“ FernUniversität, Fakultät für Mathematik und Informatik, Hagen, Germany, 2013
[2] E. Waffenschmidt und T. Staring, „Limitations of inductive power transfer for consumer applications“, in EPE – 13th European Power Electronic and Applications Conference, 2009
[3] E. Waffenschmidt, „Wireless power for mobile devices“, in INTELEC – 33rd International Telecommunications Energy Conference, 2011
[4] D. Huwig, “Inductively Coupled Power Transfer – Kontaktloser Leistungstransfer und synchrone Informationsübertragung zwischen Systemen schwacher induktiver Kopplung“, Hochschule für Technik und Wirtschaft des Saarlandes, Saarbrücken, Germany, 2007