Die zyklomatische Komplexität (cyclomatic complexity, CC) ist ein Maß aus der Graphentheorie und basiert auf dem Kontrollflussgraphen eines Stücks Software, beispielsweise einer Funktion im Sinne von C. Die zyklomatische Komplexität V(G) eines Kontrollflussgraphen wird nach der Formel
V(G) = e – n + 2 berechnet. In dieser Formel steht e für die Anzahl der (gerichteten) Kanten (edges) und n für die Anzahl der Knoten (nodes). Die Formel gilt für einen zusammenhängenden Kontrollflussgraphen. Die CC eines Kontrollflussgraphen ist die Zahl der linear unabhängigen, vollständigen Pfade durch den Graphen.
Die zyklomatische Komplexität eines Kontrollflussgraphen ist auch die Anzahl der binären (zweiwertigen) Entscheidungen plus eins. Sind n-wertige Entscheidungen im Kontrollflussdiagramm vorhanden, zählen die n-wertige Entscheidung als n-1 binäre Entscheidungen. Switch-Anweisungen mit n case-Sprungmarken mit jeweils einem folgenden Statement-Block mit abschließendem break zählen also als n-1 binäre Entscheidungen. Dazu kommt eine binäre Entscheidung für die default-Sprungmarke, egal ob diese explizit programmiert ist oder nicht.
Den Zusammenhang der zyklomatischen Komplexität V(G) mit der Anzahl der binären Entscheidungen kann man sich so veranschaulichen: Der Kontrollflussgraph einer C-Funktion ohne Verzeigungen besteht aus zwei Knoten, dem Startknoten und dem Endknoten, und einer gerichteten Kante dazwischen. Es gibt genau einen Pfad durch den Graphen. Die zyklomatische Komplexität hierfür ist V(G) = 1 – 2 + 2 = 1. Fügt man eine binäre Entscheidung in den Kontrollflussgraphen ein, ergibt sich ein weiterer linear unabhängiger Pfad und somit erhöht sich die CC um eins. Jede weitere hinzugefügte binäre Entscheidung erhöht die zyklomatische Komplexität ebenfalls um eins.
Werte mit wenig Aussagekraft
Man muss sich darüber im Klaren sein, dass der Wert der zyklomatischen Komplexität wenig über die Komplexität einer Software, beispielsweise einer C-Funktion, aussagt. Gut zu erkennen ist das an den folgenden drei Beispielen: Die zyklomatische Komplexität berücksichtigt nicht, ob eine Entscheidung zusammengesetzt ist oder nicht. In der oben stehenden Abbildung haben die Funktion func1() und func2() die gleiche zyklomatische Komplexität mit dem Wert 2, weil sie auch den gleichen Kontrollflussgraph haben. Dass dabei die Entscheidung in der if-Anweisung in der Funktion func1() eine atomare Entscheidung ist, die Entscheidung in der if-Anweisung in der Funktion func2() jedoch eine aus Bedingungen mittels logischer Operatoren zusammengesetzte Entscheidung, spielt für den Wert der zyklomatischen Komplexität keine Rolle. Ein menschlicher Betrachter würde jedoch sicherlich die Funktion func2() als komplexer einstufen.
Switch-Anweisungen sind für menschliche Betrachter oft recht übersichtlich, weil sie klar strukturiert sind. Ihre zyklomatische Komplexität ist jedoch hoch. In der Abbildung auf der nächsten Doppelseite ist auf der linken Seite eine switch-Anweisung dargestellt, die vom menschlichen Betrachter auf einen Blick erfasst und verstanden werden kann. Die zyklomatische Komplexität ist mit einem Wert von größer als 10 allerdings hoch.
Berechnungen erhöhen nicht die zyklomatische Komplexität. Auf der rechten Seite dieser Abbildung ist die Funktion sinus() dargestellt, die umfangreiche Berechnungen durchführt. Wenn man vom Funktionsnamen absieht, ist für einen menschlichen Betrachter nur schwer zu erkennen, was die Funktion berechnet, geschweige denn zu prüfen, ob sie das korrekt tut. Auch hier besteht eine große Diskrepanz zwischen dem Wert der zyklomatischen Komplexität, der 2 ist, und der für Menschen schwer nachvollziehbaren Funktionalität. Auch Zuweisungen oder Ein- und Ausgaben erhöhen die zyklomatische Komplexität nicht, obwohl sie das Verständnis der Software für Menschen erschweren.
Um diesen Fehleinschätzungen zu entgehen, empfiehlt es sich, sich an die zweite Bestimmungsmethode der zyklomatischen Komplexität zu halten. Nach dieser ist die CC die Anzahl der binären Entscheidungen plus eins. Diesen Wert sollte man allerdings nicht überinterpretieren. Hohe zyklomatische Komplexität bedeutet lediglich viele binäre Entscheidungen und niedrige zyklomatische Komplexität wenige binäre Entscheidungen.
Was die zyklomatische Komplexität besagt
Was man aus dem Wert der zyklomatischen Komplexität tatsächlich ableiten kann, ist die maximale Zahl der Testfälle, die benötigt werden, um 100 Prozent Zweigüberdeckung (branch coverage) zu erreichen. Die CC gibt die Anzahl der linear unabhängigen Pfade durch den Code an. Mehr Testfälle sind somit nicht nötig, um alle gerichteten Kanten (die Zweige) mindestens einmal auszuführen. Insofern kann man die zyklomatische Komplexität zur Abschätzung des Testaufwands zur Erreichung von 100 Prozent Zweigüberdeckung heranziehen.
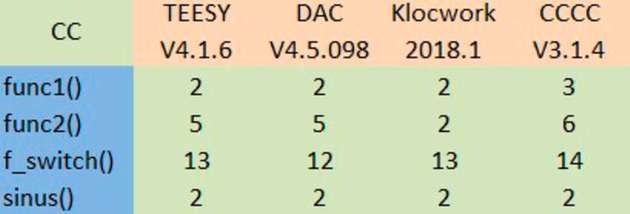
Zur Ermittlung der zyklomatischen Komplexität für reale Programme sind Werkzeuge notwendig. Solche Werkzeuge ermitteln die Metrik zyklomatische Komplexität im Rahmen der statischen Analyse der Software. Erstaunlicherweise messen nicht alle Werkzeuge die gleichen Werte für die gleichen Programmstücke. Experimente mit den kommerziellen Werkzeugen TESSY, DAC und Klocwork, sowie dem frei verfügbaren Werkzeug CCCC ergeben für die diskutierten Beispiele zum Teil unterschiedliche Werte. TESSY ist ein Werkzeug zum dynamischen Unit- und Integrationstest von Embedded Software. Die zyklomatische Komplexität wird bei der Analyse des Testobjekts quasi als Abfallprodukt mit ermittelt. DAC (Developmemt Assistant for C) ist eine integrierte Entwicklungsumgebung mit Editor, graphischer Darstellung von Aufruf-Hierarchien, Flussdiagramm- und Struktogramm-Darstellung, Prüfung von MISRA-Regeln und der Ermittlung einer Vielzahl von Metriken. Dazu gehört auch die zyklomatische Komplexität. Klocwork ist ein mächtiges statisches Analyse-Werkzeug, das C, C++, Java und C# unterstützt. Es kann außerdem Codier-Richtlinien wie MISRA, HIS, Autosar C++14 und CERT prüfen, weist auf mögliche Fehler zur Ausführungszeit hin, wie etwa NULL-Pointer-Dereferenzierung oder Zugriff außerhalb von Array-Grenzen. Zusätzlich dazu ist es in der Lage mehr als 100 Metriken zu ermitteln, darunter auch die zyklomatische Komplexität. CCCC steht für „C and C++ Code Counter“ und entstand aus einem Forschungsprojekt. Es ist über sourceforge.net frei verfügbar.
Die genannten Werkzeuge für die vier Code-Bespiele messen unterschiedlich. Beispielsweise ermitteln TESSY und DAC für die Funktion func2() den Wert 5 für die zyklomatische Komplexität, während Klocwork den Wert 2 misst. Das kann man dadurch erklären, dass TESSY und DAC für jeden der logischen Operatoren in func2() die zyklomatische Komplexität um eins erhöhen. Damit entspricht der Wert eher der „gefühlten“ Komplexität. Man kann den Wert 5 auch dadurch begründen, dass beispielsweise IF (a AND b) THEN als IF (a) THEN IF (b) THEN formuliert werden kann. Der von Klocwork gemessene Wert 2 ist der Wert der „reinen Lehre“.
Eine weitere Diskrepanz ergibt sich für die Funktion
f_switch() zwischen TESSY und Klocwork einerseits, die beide den Wert 13 messen und DAC andererseits, wo nur der Wert 12 ermittelt wird. Für die ersten drei Funktionen misst CCCC keinen Wert, der gleich wie ein Wert eines der drei anderen Werkzeuge ist. In der Dokumentation von CCCC steht dazu, dass CCCC versucht eine pragmatische Abschätzung („pragmatic approximation“) durch Zählen von Sprachelementen zu liefern. Aber auch wenn man die Regeln kennt, kann man trotzdem nicht immer nachvollziehen, wie CCCC die gemessenen Werte ermittelt hat. Die Werte von CCCC sind also mit Vorsicht zu genießen. Insgesamt geht es bei der obigen Diskussion nicht darum, was der korrekte Wert ist, sondern dass von verschiedenen Werkzeugen gelieferte Werte von einander abweichen können. Nur für die Funktion sinus() ermitteln alle vier Werkzeuge den gleichen Wert 2. Das ist korrekt, denn
sinus() besitzt nur eine binäre Entscheidung. Leider entspricht dieser Wert nicht der gefühlten Komplexität der Funktion.
Bei der Vorstellung der zyklomatischen Komplexität 1976 für die Programmiersprache Fortran empfahl der Erfinder Thomas J. McCabe, dass keine Software-Einheit einen größeren Wert als 10 haben sollte. Andernfalls sollte sie aufgeteilt werden. McCabe bezeichnet den Wert 10 als vernünftige, aber nicht von höheren Mächten vorgegebene, unantastbare obere Grenze („reasonable, but not magical, upper limit“).
Welche Werte für die zyklomatische Komplexität sollte man anstreben?
Dass eine Aufteilung der C-Funktion f_switch() aus dem obenstehenden Bild, die eine zyklomatische Komplexität von über 10 hat, nicht sinnvoll ist, versteht sich von selbst. Deshalb empfiehlt es sich, wie bei jeder anderen Metrik auch, Vergleichsdaten zu sammeln, um dadurch Ausreißer aufzuspüren. Haben beispielsweise in einem Projekt mit 100 Funktionen alle eine zyklomatische Komplexität mit Werten kleiner 20, zwei Funktionen haben jedoch Werte größer 50, so lohnt es sich, auf diese Ausreißer einen Blick zu werfen. Stellt es sich dann jedoch heraus, dass es an umfangreichen, aber klar strukturieren switch-Anweisungen liegt, kann dies akzeptiert werden. Ebenso kann man andere Projekte heranziehen: Hatte ein früheres, vergleichbares Projekt mit guter Software-Qualität niedrige Werte für die CC, das aktuelle Projekt aber nicht, so kann es eine gute Idee sein, die zyklomatische Komplexität im aktuellen Projekt zu reduzieren. McCabe hat auch festgestellt, dass die CC von Programmierer zu Programmierer unterschiedlich sein kann. Zudem muss man bedenken, dass unterschiedliche Werkzeuge offensichtlich die zyklomatische Komplexität unterschiedlich berechnen. Mit manchen Werkzeugen erhält man prinzipiell höhere Werte als mit anderen. Deshalb ist die Fixierung auf den ominösen Wert 10 fragwürdig.